Trigonometric Identity Being an ancient subject, trigonometry evolved over time and its usage is increasing continuously Thus new identities were formed from existing identitiesDOUBLEANGLE IDENTITIES sin(2x)=2sin(x)cos(x) cos(2x) = cos2(x)sin2(x) = 2cos2(x)1 =12sin2(x) tan(2x)= 2tan(x) 1 2tan (x) HALFANGLE IDENTITIES sin ⇣x 2 ⌘ = ± r 1cos(x) 2 cos ⇣x 2 ⌘ = ± r 1cos(x) 2 tan ⇣x 2 ⌘ = ± s 1cos(x) 1cos(x) PRODUCT TO SUM IDENTITIES sin(x)sin(y)= 1 2 cos(xy)cos(xy) cos(x)cos(y)= 1 2 cos(xy)cos(xyMar 21, 19 · 71 Solving Trigonometric Equations with Identities For the exercises 16, find all solutions exactly that exist on the interval \(0,2\pi )\) 1) \(\csc ^2 t=3\)
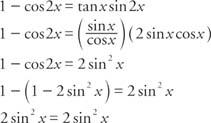
Double Angle And Half Angle Identities
Trig identities tan(x/2)
Trig identities tan(x/2)-Source Trigonometry identities Math Open Reference A Reciprocal identities a1 sin A=1 csc A a4 csc A=1 sin A a2 cos A=1 sec A a5 sec A=1 cos A a3 tan A=1 cot A a6 cot A=1 tan A B Ratio identities b1 tan A= sin A cos A b2 cot A= cos A sin A COct 18, 16 · How do you apply the fundamental identities to values of #theta# and show that they are true?
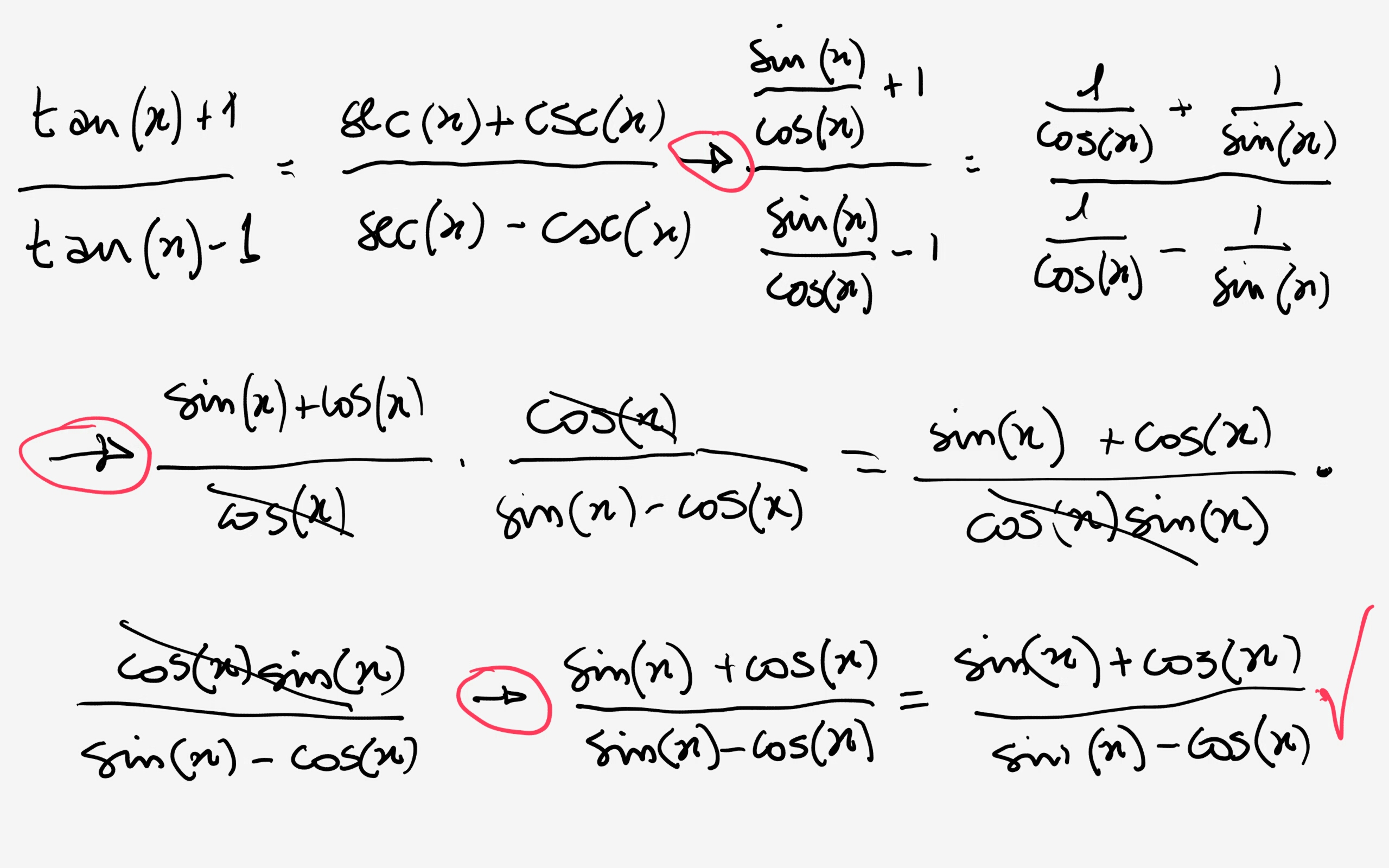


How Do You Prove Tan X 1 Tan X 1 Sec X Csc X Sec X Csc X Socratic
Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 pWhat are even and odd functions?Recall the definitions of the trigonometric functions The following indefinite integrals involve all of these wellknown trigonometric functions Some of the following trigonometry identities
2 The Elementary Identities Let (x;y) be the point on the unit circle centered at (0;0) that determines the angletrad Recall that the de nitions of the trigonometric functions for this angle are sint = y tant = y x sect = 1 y cost = x cott = x y csct = 1 x These de nitions readily establish the rst of the elementary or fundamental identities given in the table belowNov 09, · Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identities mostly refer to one angle labelled $Feb 07, 21 · All of the trigonometric functions can be rewritten in terms of only \(x\), when using one of the inverse trigonometric functions Starting with tangent, we draw a triangle where the opposite side (from \(\theta \)) is defined as \(x\) and the adjacent side is 1
May 26, · Just remember that in order to use the trig identities the coefficient of the trig function and the number in the identity must be the same, ie both 4 or 9, so that the trig identity can be used after we factor the common number out What this means is that we need to "turn" the coefficient of the squared term into the constant number3x 2x = 5x is an identity that is always true, no matter what the value of x, whereas 3x = 15 is an equation (or more precisely, a conditional equation) that is only true if x = 5 A Trigonometric identity is an identity that contains the trigonometric functions sin, cos, tan, cot, sec or csc Trigonometric identities can be used toUsing Trig Identities, factoring, and Unit Circle Angles Tan X cot X 2 Tan Xl = X Tan X 2TanX1 (Tan X x 1) 0 Sec X Step 1 I want to get lid of the inverse (CotX) Multiply everything by TanX Step 2 Move everything to one side and factor Step 3 Find solutions and check Tan (45) Tan


Answered Trigonometric Identities And Equations Bartleby
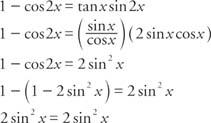


Double Angle And Half Angle Identities
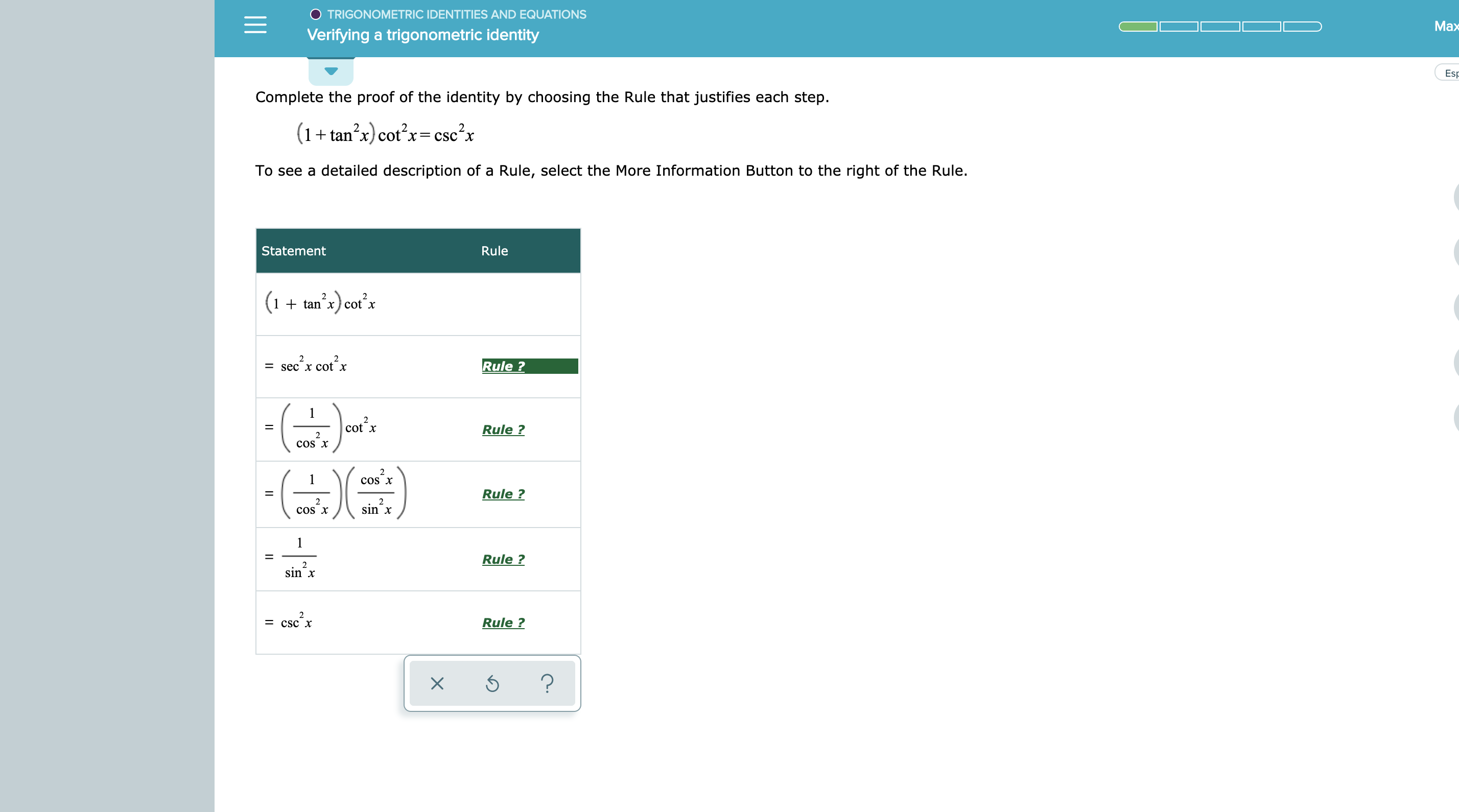
• We will analyze trigonometric identities numerically and graphically • We will discuss techniques used to manipulate and simplify expressions in order to prove trigonometric identities algebraically Recall A trigonometric identity is an equation formed by the equivalence of two trigonometric expressionsType your expression into the box to the right Your expression may contain sin, cos, tan, sec, etc When you click the button, this page will try to apply 25 different trig identities that it knows about to simplify your expression As an example, try typing sin(x)^2cos(x)^2 and see what you get3) Use trig identities to simplify and then determine which of the following is NOT equivalent csc x tan x sec x A) cscxsinx secxcosx cosx B)2 tan x C) 2 sec x D) 2tanx sinx 4) Use trig identities to simplify tan2x cot2x A) sec2x 1 B) sec2x csc2x C) csc2x sec2x D) 1



Trig Integrals Trig Substitution
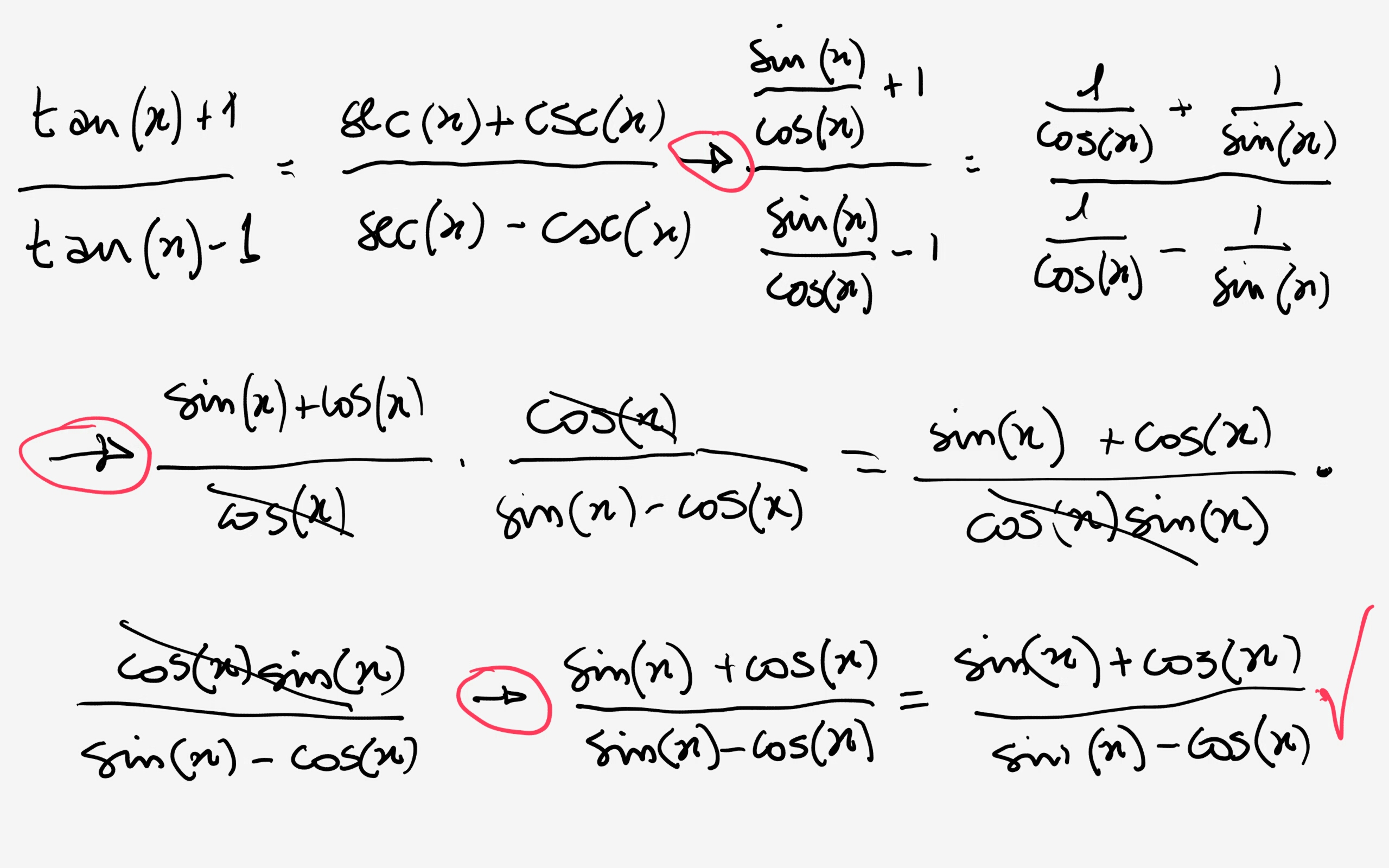


How Do You Prove Tan X 1 Tan X 1 Sec X Csc X Sec X Csc X Socratic
To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x The preceding three examples verify three formulas known as the reductionIn this section we use trigonometric identities to integrate certain combinations of trigonometric functions We start with powers of sine and cosine tan2x 2 ln sec x C y tan x sec2x dx y tan x dx y tan x sec 2x 1 dx y tan3x dx y tan x tan2x dx sec2x tan x tan2x sec2x 1 tan2x y tan3x dx y sec x dx ln sec x tan x C481 Trig identities vs trig equations What is a trig identity?



Trigonometry Reciprocal Identities Expii



Integrate Sec 2x Method 1
Jan 21, 19 · Remember that when proving an identity, work to transform one side of the equation into the other using known identities Some general guidelines are Begin with the more complicated side It is often helpful to use the definitions to rewrite all trigonometric functions in terms of the cosine and sine When appropriate, factor or combine termsThis is probably the most important trig identity Identities expressing trig functions in terms of their complements There's not much to these Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent andExample 1 Compute Z 1 p x2 9 dx Soluionp Here, no usubstitution will work, and so we use trig sub From the above table, we have x 229 = p px 3 , so letting x = 3sec and dx = 3sec tan d transforms the square root into



Weierstrass Substitution Wikipedia


Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
Examples of such expressions are $$ \displaystyle{ \sqrt{ 4x^2 }} \ \ \ and \ \ \ \displaystyle{(x^21)^{3/2}} $$ The method of trig substitution may be called upon when other more common and easiertouse methods of integration have failedIntroduction This is a continuation of the first blog on Trigonometric Identities, we recommend you to read that first To visit that please click here Trigonometric Identities Part 1 Most of us find it difficult to understand Trigonometry as it's hard to remember so many related formulae and functionsHow do you use the fundamental identities to prove other identities?



How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic



Worksheet On Trigonometric Identities Establishing Identities Hints
62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Quotient identity Quotient identityIdentities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal DistributionJan 07, 11 · In integral calculus, the Weierstrass substitution or tangent halfangle substitution is a method for evaluating integrals, which converts a rational function of trigonometric functions of into an ordinary rational function of by setting = (/) No generality is lost by taking these to be rational functions of the sine and cosine The general transformation formula is



Solved 2 Prove The Following Trig Identities A Prove Chegg Com



Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube
Times New Roman Arial Calibri Symbol Default Design 51 Fundamental Trig Identities 51 Practice Problems Identity Matching Practice More Identity Matching Practice More Practice 52 Verifying Identities Verify the Following Identities Verify more challenging Identities 53 & 54 Sum and Difference Formulas 53 & 54 Practice Problems 55 & 5The best videos and questions to learn about HalfAngle Identities Get smarter on SocraticList of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) andcos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ andcos θ The tangent (tan) of an angle is the ratio of the sine to the cosine
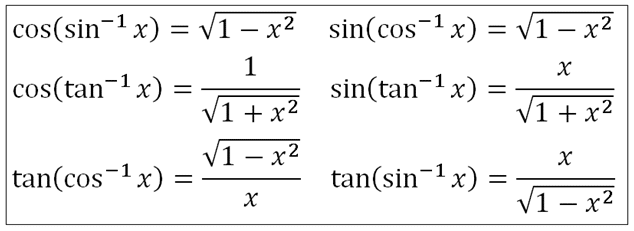


Inverse Trig Identities Reciprocal Of Trigonometric Function Trig



Trigonometric Identities A Plus Topper
Basic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian planeTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1Trigonometric Identities 43 Introduction A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an application
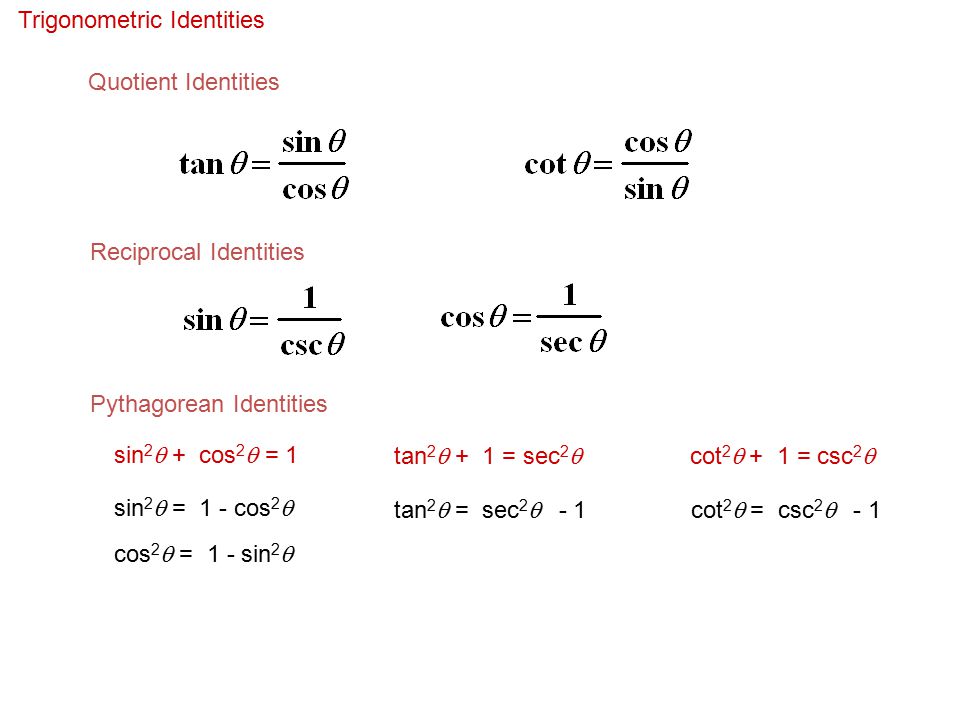


11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



Solved Which Of The Following Is Not A Trigonometric Iden Chegg Com
Trig identities or a trig substitution mcTYintusingtrig091 Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities These allow the integrand to be written in an alternative form which may be more amenable to integrationA trig identity is an equation which is true for all inputs (such as angles, ) For example, from the Pythagorean theorem on the unit circle, we know that the equation for the unit circle is x 2 y = 1 and so this turns into an identity for trig functions cos2 sin2 = 1 This isTrig identities are trigonometry equations that are always true, and they're often used to solve trigonometry and geometry problems and understand various mathematical properties Knowing key trig identities helps you remember and understand important mathematical principles and solve numerous math problems



How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
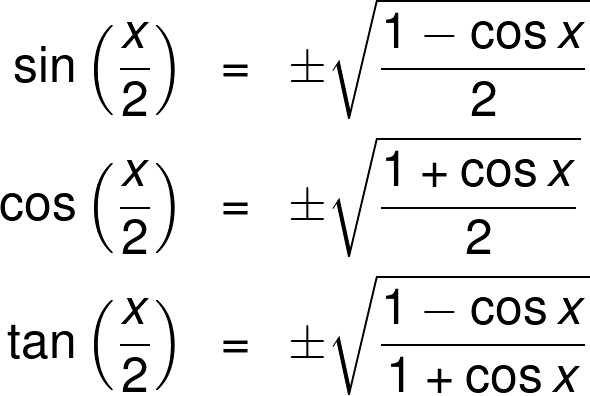


Half Angle Calculator
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience ByBasic trigonometric identities Common angles Degrees 0 30 45 60 90 Radians 0 tan(2x) = 2tanx 1 tan2 x 2 Half angles sin x 2 = r 1 cosx 2 cos x 2 = r 1cosx 2 tan x 2 = 1 cosx sinx = sinx 1cosx Power reducing formulas sin2 x= 1 cos2x 2 cos2 x= 1cos2x 2 tan2 x= 1The inverse trigonometric identities or functions are additionally known as arcus functions or identities Fundamentally, they are the trig reciprocal identities of following trigonometric functions Sin Cos Tan These trig identities are utilized in circumstances when the area of the domain area should be limited These trigonometry functions have extraordinary


Summary Of Trigonometric Identities


How Do You Simplify The Identify Sin 2x 1 Cosx 1 Cosx Socratic
Trigonometric integrals span two sections, another page on integrals containing only trigonometric functions, and this page integration of specific algebraic functions by substitution of variables with trig functions Both are useful, so make sure to check out the first, tooImportant trig identities First we recall the Pythagorean identity If we begin with the cosine double angle formula, we can use the Pythagorean identity to substitute 1 cos 2 θ for sin 2 θ to obtain one of the powerreduction identities Notice that this identity allows us downconvert the power of the cosine function from 2 to 1
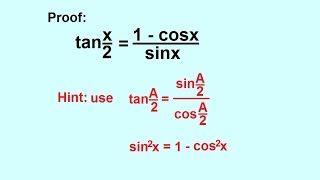


Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



11 Tips To Conquer Trigonometry Proving



Summary Of Trigonometric Identities



Trigonometric Identities Ppt Video Online Download


6 1 2 Trigonometric Identities



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
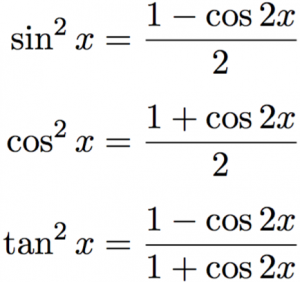


Trig Identities Table Of Trigonometric Identities


Derivatives Of Trigonometric Functions



Trigonometric Identities A Plus Topper


Ilectureonline



Tangent Half Angle Formula Wikipedia
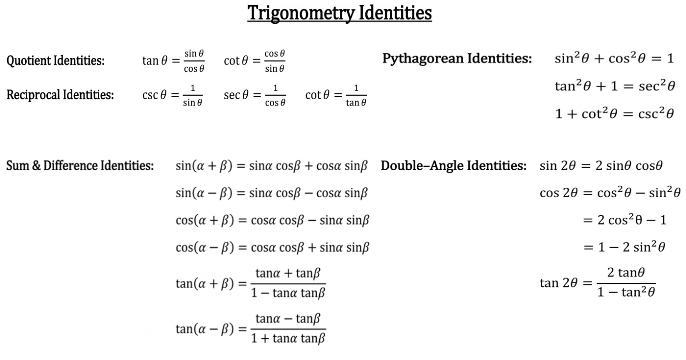


How To Prove Quotient And Reciprocal Identities Studypug



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



How To Use Trig Identities Mathematics Stack Exchange


A Trig Identity



Trigonometric Identities Practice Problems Key



Verifying A Trigonometric Identity Tan X Sec X Sin X Youtube



Trig Identities Homework Help Working With Trigonometric Identities


10 4 Integration Of Powers Of Trigonometric Functions



Trig Double Identities Trigonometric Double Angle Functions Trig


Trig Identities Bingo Card


What Are The Quotient Identities For A Trigonometric Functions Socratic



Solved Verify The Identity 1 Tan X 2 Sec 2 X 2 Tan Chegg Com



Trig Identities Bingo Card



Powers Of Trigonometric Functions



Chapter 7 Analytic Trigonometry
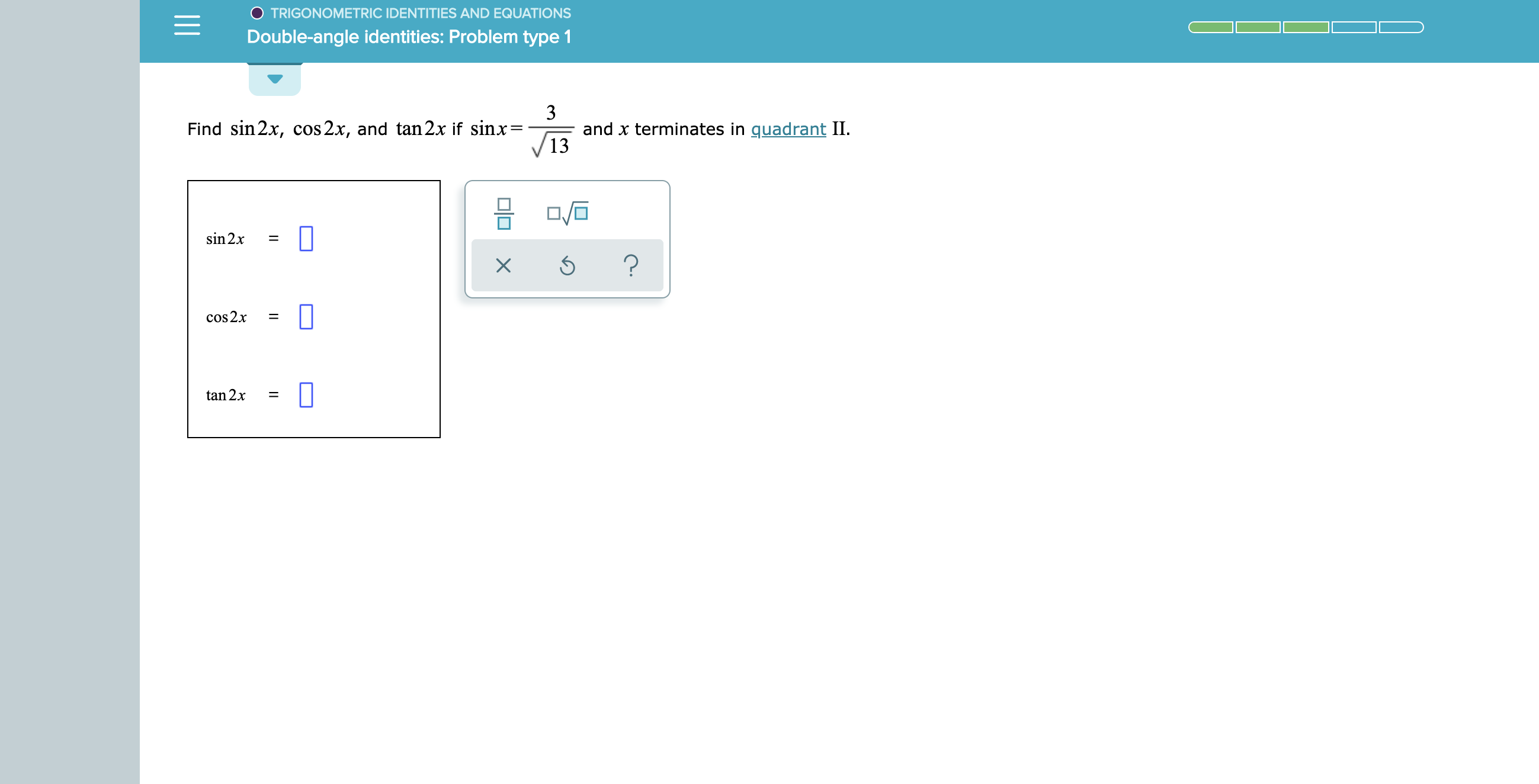


Answered Trigonometric Identities And Equations Bartleby



Using Trigonometric Identities Video Khan Academy



Trigonometric Identity 1 Sin X 1 Sin X Sec X Tan X 2 Cbse 10 Youtube


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



Verify A Trigonometric Identity Ppt Video Online Download


Trig Identities Hsn Forum



7 1 Notes



Summary Of Trigonometric Identities



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions


What Does It Mean To Prove A Trigonometric Identity Socratic



Tangent Half Angle Formula Wikipedia


7 Proving Ids Trig Functions Identities


6 1 2 Trigonometric Identities


Solved Find The Remaining Five Trigonometric Functions Of 0 See Example 1 Sin A 0 In Quadrant Ii 32 Cos 0 0 In Quadrant I 33 Tan 0 Course Hero



Trig Identities Worksheet With Answers 2



6 3 Trig Identities Ppt Video Online Download



Ppt Basic Trig Identities Sin 2 X Cos 2 X 1 Powerpoint Presentation Id


Integrate Sec 2x Method 2



Ch 7 Trigonometric Identities And Equations Ppt Video Online Download



Ppt Analytic Trig Powerpoint Presentation Free Download Id



Weierstrass Substitution Wikipedia



5 1 Fundamental Trig Identities Reciprocal Identities Sin



How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Solved Simplify Each Of The Following Trigonometric Expre Chegg Com


Biomath Trigonometric Functions


Bestmaths Online Proof 4



Which Of The Following Expressions Completes The Identity 1 Sec 2 X Mathematics Stack Exchange


How I Choose Which Trig Substitution To Do Making Your Own Sense


Summary Of Trigonometric Identities



How To Prove Quotient And Reciprocal Identities Studypug



List Of Trigonometric Identities Wikipedia


Trig Identities Hsn Forum



Solved Verify The Identity Tan X Cot X 2 Csc 2 X Chegg Com



Integrate Sec 2x Method 2



Alternate Forms Of Trigonometric Identities Video Lesson Transcript Study Com



Solved We Wish To Prove The Following Trig Identity Tan Chegg Com
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com
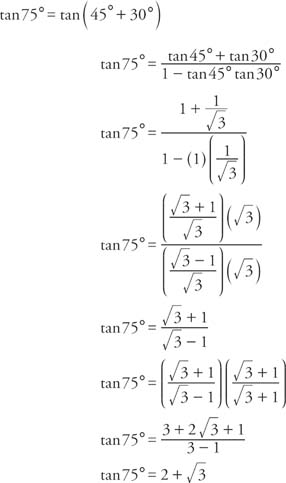


Tangent Identities


Trig Identities Crossword Wordmint


Summary Of Trigonometric Identities


What Is The Identity Tan 2x Equal To In Terms Of Sinx And Cosx Quora



7 4 Proving Trigonometric Identities Mhf4utrigonometry



Establishing Conditional Results Using Trigonometric Identities Hints



Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
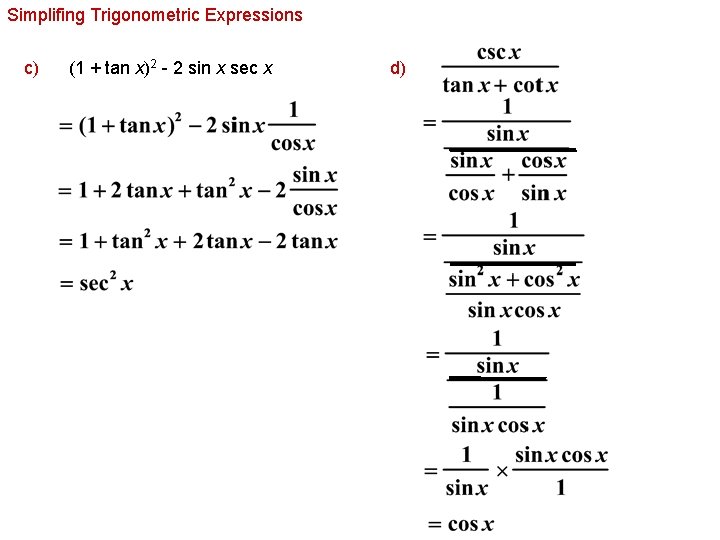


While You Wait Trigonometric Identities And Equations Section



Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities


What Is Sec X Tan X 2 1 Sin X 1 Sin X Quora



7 4 Proving Trigonometric Identities In This Unit We Ll Be Using Some Formula S That Are Also Found And Used In Unit 7 2 And 7 3 Here We Ll Be Solving Problems To Show That Both Sides Of The Equation Equal Each Other These Formulas Will Help Solve Some Trig



Solved 2 Prove The Following Trig Identities A Prove Chegg Com



0 件のコメント:
コメントを投稿